More About CG Placement - Mean Aerodynamic Chord

 

Last time, we learned that every aircraft configuration has an "aerodynamic center" (AC), a point where a change in lift will appear when angle of attack (AoA) changes.  If we can locate this point, we can make the airplane stable in pitch by putting the CG ahead of it.  For simple (constant wing and stabilizer chord) designs, we can find the AC figuring the "tail volume coefficient" (V_bar) and using the chart above.

Pretty simple - but what about more complex designs?  Such as swept and tapered wings, or biplanes?

It turns out we can still use the "tail volume" idea, but we need to think in terms of "mean aerodynamic chord" (MAC).

What the heck is MAC?  Well, it turns out MAC has both a length and a location.

Finding the length is easy, just the wing area divided by the span:

        c_bar = S/b

(Don't ask me why, but some sadist decided decades ago to use "S" for wing area, and "b" for wingspan. It's a universal convention for aeronautical engineers, so readers get to suffer as well.)

Finding the location is a little trickier.  The MAC of a surface is the chord line along which our change in lift will appear.  So, it turns out that the MAC is chord which divides the surface into equal areas:

Notice that the MAC will not be in the same place as the root chord.  Sweeping the wing back moves the MAC back; sweeping it forward pulls it forward.  Tapering the wing moves the MAC toward the root chord.  If there is no taper, it will be halfway toward the tip.  If the wing is a true delta (zero tip chord), it will be one third of the way toward the tip.

So the concept is simple.  The wing has its MAC, the stab has a different MAC.  Project the quarter chord of each surface's MAC onto the root chord and you have the AC of that surface.  Measure the distance between these ACs and you have the tail lever arm, and can use the formula and chart from last time to find the aircraft AC.

In practice - it's not quite that simple.

Since a MAC divides a wing panel into equal areas, one way of finding it is to trace your wing onto squared paper.  Then start counting squares from either end, and stop when you find a chord line with equal numbers of squares on each side.  Have fun pulling your hair out with that one.

If your wing or stab has straight leading and trailing edges, you can use a fairly simple graphical method to locate the MAC:

You can measure the length ("c_bar" is the "c" with the bar drawn over it), or if you're feeling really persnickety, you can use these "simple" formulas to calculate it:

But most of us would probably rather suffer through a colonoscopy, or file an extra income tax return, than go through all of that.

Is there a simpler way?

It turns out there is:  an online CG calculator!

These programs do all the work for you.  Using your measurements (on the model, or your plans) they divide the wing and stab into a number of polygons.  Applying the math concepts above, they find the MAC, AC and area of each polygon, add them all up, massage the numbers and come out with the answer.  And because they've usually been "debugged" the chance of them making a math error is much lower than a hand calculation.

One of them I like lives here:

eCalc - cgCalc - Center of Gravity (CG) Calculator for RC airplane, flying wing, delta or canard

This one was developed by Markus Mueller, a modeller (and airline captain) from Switzerland.  It can handle up to five polygons per wing (and stab) panel, and also works for canards and biplanes.  It draws a little diagram of the plane as you work, so you can see at a glance whether you've fallen victim to "garbage in, garbage out" with your measurements.  And you can work in inches rather than centimeters!

It's not free (at least if you want the full version), but the cost is only about $1.50 per month.  And that doesn't just get you the CG calculator, but a whole package of useful spreadsheets for things like electric power systems, aircraft performance, and helicopters.  If you're at all serious about designing your own models, scratchbuilding power systems, or even tuning up out of the box planes it's well worth considering.

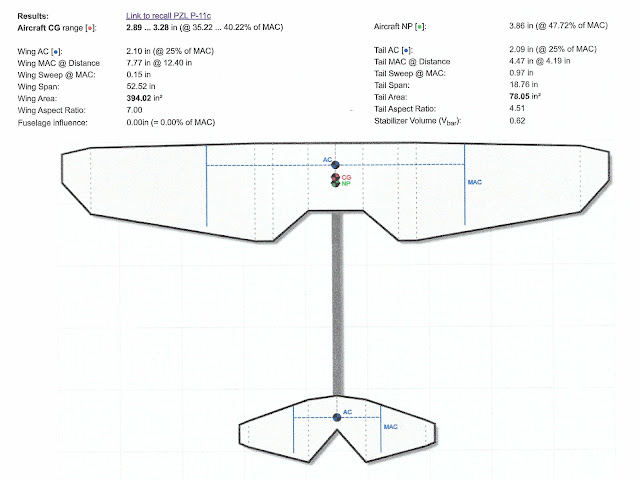
Let's see how cg_Calc did with my PZL P-11c:

First, the measurements you need to take.  Each surface is based on its root chord (R).  From there, each polygon (or "panel") has a "sweep" (S), a "tip chord" (T), and a "span" (W) as shown in the diagram.  For the lever arm, Markus has you go from the leading edge of the wing root chord to the leading edge of the stab root chord; he'll find the MAC locations for you.  You can get all the numbers in just a few minutes, using a straightedge and tape measure!

And now the PZL results:

This is a pretty complex shape, with the center section cutouts and both surfaces swept and tapered.  The rounded wing tips aren't exact but they don't contribute that much to the total area.  It would be pretty hard to do better than this using a hand calculation or graphical method.

Now we have a method anyone can use!  So what is it telling us?

The points marked "AC" (blue text) are the aerodynamic centers of the wing and stab

The point marked "NP" (green text) is the aircraft aerodynamic center. "NP" stands for "Neutral Point", or point of neutral pitch stability.  That's because if we balance the model at the NP, it will be neither stable nor unstable in pitch.

The point marked "CG" (red text" is the recommended CG location.  As you can see, it's some distance forward of the NP - depending on how much "static margin" the user selects in cg_Calc.

Now, just what the heck is "static margin"?

More to follow next time...